All Important Trigonometry Formula for Class 10, Check Examples

All Important Trigonometry Formula for Class 10: Candidates can check all important Trigonometry formulas for class 10 in this article. Trigonometry is the study of the relationship between angles, lengths, and heights of triangles. Trigonometry includes ratios, identities, functions, and formulas to solve problems based on it. Engineering, Astronomy, Architectural design, and Physics also include Applications of Trigonometry. Students need to memorize trigonometry formulas by practicing problems. 

Students are introduced to Trigonometry formulas in CBSE class 10. This chapter is very tricky so students need to learn all the formulas and apply them accordingly. All Important Trigonometry Formula for Class 10 is given below

Trigonometry Formula for Class 10

Physics Wallh has provided all the important Maths trigonometry formulas that students need to study in CBSE class 10. Trigonometry formulas are majorly based on three sides of a right triangle i.e., adjacent side, base, and hypotenuse. According to the Pythagoras theorem,

(Perpendicular)2+ (Base)2 = (Hypotenuse)2

(P)2 + (B)2 = (H)2

Candidates can check the formulas based on trigonometry ratios below

Basic Trigonometry Formulas 

Candidates can check the basic trigonometry formulas for CBSE class 10 students in the table below

Check out: CBSE Class 10th Question Banks

Relation Between Trigonometric Ratios

Students can check the relation between the Trigonometric Ratios in the table below. 

MathsTrigonometry Sign Functions

• sin (-θ) = − sin θ

• cos (−θ) = cos θ

• tan (−θ) = − tan θ

• cosec (−θ) = − cosec θ

• sec (−θ) = sec θ

• cot (−θ) = − cot θ

Trigonometric Identities

• sin2A + cos2A = 1

• tan2A + 1 = sec2A

• cot2A + 1 = cosec2A

Check out: CBSE Class 10th Previous Year Papers

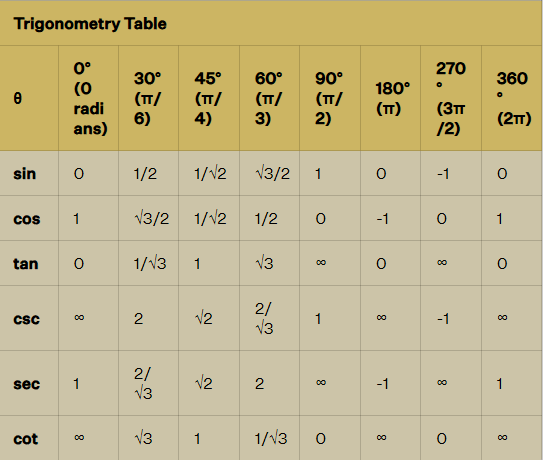
Trigonometry Table Formula: Trigonometric Ratio Table

Students can check the table for Trigonometric formulas for angles that are commonly used for solving Trigonometry problems. This ratio table will help in finding the values of Trigonometric standard angles such as 0°, 30°, 45°, 60°, and 90°.

 

Trigonometry Periodic Identities (in Radians)

In important Trigonometry formulas for class 10, periodic identities are used to shift the angles by π/2, π, 2π, etc. After a period, every trigonometry formula repeats itself. This period differs for different trigonometry formulas on periodic identities. For example, tan 30° = tan 210° but cos 30° not equal to cos 210°.

First Quadrant:

• sin (π/2 – θ) = cos θ

• cos (π/2 – θ) = sin θ

• sin (2π + θ) = sin θ

• cos (2π + θ) = cos θ

Second Quadrant:

• sin (π/2 + θ) = cos θ

• cos (π/2 + θ) = – sin θ

• sin (π – θ) = sin θ

• cos (π – θ) = – cos θ

Third Quadrant:

• sin (π + θ) = – sin θ

• cos (π + θ) = – cos θ

• sin (3π/2 – θ) = – cos θ

• cos (3π/2 – θ) = – sin θ

Fourth Quadrant:

• sin (3π/2 + θ) = – cos θ

• cos (3π/2 + θ) = sin θ

• sin (2π – θ) = – sin θ

• cos (2π – θ) = cos θ

Check Out: CBSE Class 10th Sample Papers

Sum and Difference of Two Angles

• sin (A + B) = sin A cos B + cos A sin B

• sin (A − B) = sin A cos B – cos A sin B

• cos (A + B) = cos A cos B – sin A sin B

• cos (A – B) = cos A cos B + sin A sin B

• tan(A + B) = [(tan A + tan B) / (1 – tan A tan B)]

• tan(A – B) = [(tan A – tan B) / (1 + tan A tan B)]

Double Angle Formulas

• sin 2A = 2 sin A cos A = [2 tan A /(1 + tan2A)]

• cos 2A = cos2A – sin2A = 1 – 2 sin2A = 2 cos2A – 1 = [(1 – tan2A)/(1 + tan2A)]

• tan 2A = (2 tan A)/(1 – tan2A)

Triple Angle Formulas

• sin 3A = 3 sinA – 4 sin3A

• cos 3A = 4 cos3A – 3 cos A

• tan 3A = [3 tan A – tan3A] / [1 − 3 tan2A]

Check out: School Prep Books

Solved Examples Using Important Trigonometry Formulas for Class 10

Students from CBSE class 10 can refer to the below examples which are based on trigonometry formulas. Students may get this type of problem during the examination

Q1. If cot Q = tan P then prove that P + Q = 90°.

Ans. Given,

tan P = cot Q

As we know, cot(90° – A) = Tan A.

So, cot Q = cot(90° – P)

Therefore, Q = 90° – P

And

P + Q = 90°

Hence proved.

Q2. Evaluate cos 55° sin 35° + cos 35° sin 55°.

Ans. Given expression:

cos 55° sin 35° + cos 35° sin 55°

The above equation is in the form sin A cos B + cos A sin B.

Now, using sin(A + B) = sin A cos B + cos A sin B, we get;

cos 55° sin 35° + cos 35° sin 55° = sin(35° + 55°) = sin 90° = 1

Q3. If sin A = 3/5, then find the value of cos A and cot A

Ans. Sin A = 3/5

Now, sin2A + cos2A = 1

cos2A = 1- (⅗)2

= (25 - 9) / 25

= 16 / 25

cos A = 4/5

Also, cot A = cosA / sinA

= (4/5)(3/5)

= 4/3

Trigonometry Formula for Class 10- FAQs

Q1. How many total formulas are there in trigonometry class 10?

Ans. There are six trigonometric functions such as sine, cosine, secant, cosecant, tangent, and cotangent. By using a right-angled triangle as a reference, sin θ = Opposite Side/Hypotenuse. cos θ = Adjacent Side/Hypotenuse. 

Q2. What are the 3 golden formulas of trigonometry?

Ans. The 3 golden formulas of trigonometry are sin2A + cos2A = 1. 1 + tan2A = sec2A. 1 + cot2A = cosec2A.

Q3. Who is the father of trigonometry?

Ans. The father of trigonometry is Hipparchus, a Greek mathematician who discovered trigonometry in the second century BC. 

Q4. What are the two types of trigonometry?

Ans. The two types of trigonometry are Plane Trigonometry and Spherical Trigonometry. 

Q5. What is the maximum and minimum value of sinθ?

Ans. The maximum value of sinθ is 1 and the minimum value of sinθ is -1.