NCERT Solutions For Class 12 Physics Chapter 13 Nuclei

Nuclei class 12 ncert solutions provide a comprehensive framework for understanding the central core of atoms. These detailed class 12 physics chapter 13 nuclei questions answers help you master complex topics like mass-energy equivalence, nuclear force, and radioactivity. By using these solutions, students can effectively navigate the numerical problems and theoretical concepts required to excel in their upcoming CBSE board examinations and competitive tests.

Check Out: CBSE Class 12 Books

Class 12 Physics Chapter 13 Nuclei Questions Answers

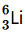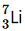Question 1. (a) Two stable isotopes of lithiumandhave respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium. (b) Boron has two stable isotopes,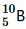and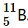. Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of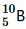and.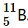 

Solution : (a) Mass of lithium isotope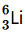, m1 = 6.01512 u Mass of lithium isotope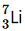, m2 = 7.01600 u Abundance of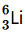, η1= 7.5% Abundance of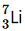, η2= 92.5% The atomic mass of lithium atom is given as:== 6.940934 u. (b) Mass of boron isotope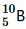, m1 = 10.01294 u Mass of boron isotope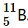, m2 = 11.00931 u Abundance of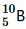, η1 = x% Abundance of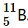, η2= (100 − x)% Atomic mass of boron, m = 10.811 u The atomic mass of boron atom is given as:x = 19.821/0.99637 = 19.89% And 100 − x = 80.11% Hence, the abundance of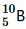is 19.89% and that of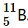is 80.11%.

Question 2. The three stable isotopes of neon: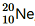,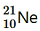andhave respective abundances of 90.51%, 0.27% and 9.22%. The atomic masses of the three isotopes are 19.99 u, 20.99 u and 21.99 u, respectively. Obtain the average atomic mass of neon. 

Solution : Atomic mass of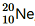, m1= 19.99 u Abundance of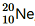, η1 = 90.51% Atomic mass of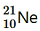, m2 = 20.99 u Abundance of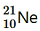, η2 = 0.27% Atomic mass of, m3 = 21.99 u Abundance of, η3 = 9.22% The average atomic mass of neon is given as:= 20.1771u 

Question 3. Obtain the binding energy (in MeV) of a nitrogen nucleus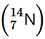, given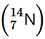=14.00307 u 

Solution : Atomic mass of nitrogen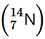, m = 14.00307 u A nucleus of nitrogen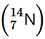contains 7 protons and 7 neutrons. Hence, the mass defect of this nucleus, Δm = 7mH + 7mn − m Where, Mass of a proton, mH = 1.007825 u Mass of a neutron, mn= 1.008665 u ∴Δm = 7 × 1.007825 + 7 × 1.008665 − 14.00307 = 7.054775 + 7.06055 − 14.00307 = 0.11236 u But 1 u = 931.5 MeV/c2 ∴Δm = 0.11236 × 931.5 MeV/c2 Hence, the binding energy of the nucleus is given as: Eb = Δmc2 Where, c = Speed of light ∴Eb = 0.11236 × 931.5 (MeV/c2) = 104.66334 MeV Hence, the binding energy of a nitrogen nucleus is 104.66334 MeV.

Question 4. Obtain the binding energy of the nuclei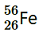and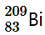in units of MeV from the following data: m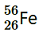= 55.934939 u  m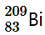= 208.980388 u 

Solution : Atomic mass of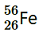, m1 = 55.934939 u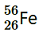nucleus has 26 protons and (56 − 26) = 30 neutrons Hence, the mass defect of the nucleus, Δm = 26 × mH + 30 × mn − m1 Where, Mass of a proton, mH = 1.007825 u Mass of a neutron, mn = 1.008665 u ∴Δm = 26 × 1.007825 + 30 × 1.008665 − 55.934939 = 26.20345 + 30.25995 − 55.934939 = 0.528461 u But 1 u = 931.5 MeV/c2 ∴Δm = 0.528461 × 931.5 MeV/c2 The binding energy of this nucleus is given as: Eb1 = Δmc2 Where, c = Speed of light ∴Eb1 = 0.528461 × 931.5 (MeV/c2) = 492.26 MeV Average binding energy per nucleon 492.26/56 = 8.79 MeV Atomic mass of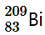, m2 = 208.980388 u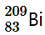nucleus has 83 protons and (209 − 83) 126 neutrons. Hence, the mass defect of this nucleus is given as: Δm' = 83 × mH + 126 × mn − m2 Where, Mass of a proton, mH = 1.007825 u Mass of a neutron, mn = 1.008665 u ∴Δm' = 83 × 1.007825 + 126 × 1.008665 − 208.980388 = 83.649475 + 127.091790 − 208.980388 = 1.760877 u But 1 u = 931.5 MeV/c2 ∴Δm' = 1.760877 × 931.5 MeV/c2 Hence, the binding energy of this nucleus is given as: Eb2 = Δm'c2 = 1.760877 × 931.5(MeV/c2) = 1640.26 MeV Average bindingenergy per nucleon = 1640.26/209 = 7.848 MeV

Question 5. A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of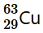atoms (of mass 62.92960 u). 

Solution : Mass of a copper coin, m’ = 3 g Atomic mass of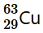atom, m = 62.92960 u The total number of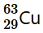atoms in the coinWhere, NA = Avogadro’s number = 6.023 × 1023 atoms /g Mass number = 63 g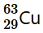nucleus has 29 protons and (63 − 29) 34 neutrons ∴Mass defect of this nucleus, Δm' = 29 × mH + 34 × mn − m Where, Mass of a proton, mH = 1.007825 u Mass of a neutron, mn = 1.008665 u ∴Δm' = 29 × 1.007825 + 34 × 1.008665 − 62.9296 = 0.591935 u Mass defect of all the atoms present in the coin, Δm = 0.591935 × 2.868 × 1022 = 1.69766958 × 1022 u But 1 u = 931.5 MeV/c2 ∴Δm = 1.69766958 × 1022 × 931.5 MeV/c2 Hence, the binding energy of the nuclei of the coin is given as: Eb= Δmc2 = 1.69766958 × 1022 × 931.5 (MeV/c2) = 1.581 × 1025 MeV But 1 MeV = 1.6 × 10−13 J Eb = 1.581 × 1025 × 1.6 × 10−13 = 2.5296 × 1012 J This much energy is required to separate all the neutrons and protons from the given coin.

uestion 6. Write nuclear reaction equations for (i) α-decay of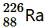(ii) α-decay of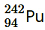(iii) β−-decay of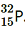(iv) β−-decay of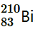(v) β+-decay of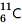(vi) β+-decay of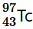(vii) Electron capture of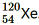

Solution : α is a nucleus of heliumand β is an electron (e− for β− and e+ for β+). In every α-decay, there is a loss of 2 protons and 4 neutrons. In every β+-decay, there is a loss of 1 proton and a neutrino is emitted from the nucleus. In every β−-decay, there is a gain of 1 proton and an antineutrino is emitted from the nucleus. For the given cases, the various nuclear reactions can be written as:

Question 7. A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to a) 3.125%, b) 1% of its original value? 

Solution : Half-life of the radioactive isotope = T years Original amount of the radioactive isotope = N0 (a) After decay, the amount of the radioactive isotope = N It is given that only 3.125% of N0 remains after decay. Hence, we can write:Where, λ = Decay constant t = TimeHence, the isotope will take about 5T years to reduce to 3.125% of its original value. (b) After decay, the amount of the radioactive isotope = N It is given that only 1% of N0 remains after decay. Hence, we can write:Hence, the isotope will take about 6.645T years to reduce to 1% of its original value.

Question 8. The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive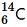present with the stable carbon isotope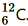. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of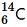, and the measured activity, the age of the specimen can be approximately estimated. This is the principle of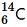dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation. 

Solution : Decay rate of living carbon-containing matter, R = 15 decay/min Let N be the number of radioactive atoms present in a normal carbon- containing matter. Half life of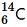,= 5730 years The decay rate of the specimen obtained from the Mohenjodaro site: R' = 9 decays/min Let N' be the number of radioactive atoms present in the specimen during the Mohenjodaro period. Therefore, we can relate the decay constant, λand time, t as:Hence, the approximate age of the Indus-Valley civilisation is 4223.5 years.

Question 9. Obtain the amount of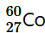necessary to provide a radioactive source of 8.0 mCi strength. The half-life of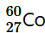is 5.3 years. 

Solution : The strength of the radioactive source is given as: dN/dt = 8.0mCi Where, N = Required number of atoms Half-life of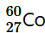,= 5.3 years = 5.3 × 365 × 24 × 60 × 60 = 1.67 × 108 s For decay constant λ, we have the rate of decay as:For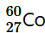: Mass of 6.023 × 1023 (Avogadro’s number) atoms = 60 g ∴Mass of 7.133 x 10 ¹⁶ atoms = 60 x 7.133 x 10 ¹⁶ /6.023 x 10 ²³ = 7.106 x 10 ^-6 g Hence, the amount of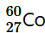necessary for the purpose is 7.106 × 10−6 g.

Question 10. The half-life of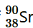is 28 years. What is the disintegration rate of 15 mg of this isotope?

 Solution : Half life of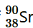,= 28 years = 28 × 365 × 24 × 60 × 60 = 8.83 × 108 s Mass of the isotope, m = 15 mg 90 g of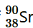atom contains 6.023 × 1023 (Avogadro’s number) atoms. Therefore, 15 mg of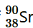contains:Rate of disintegration,Where,Hence, the disintegration rate of 15 mg of the given isotope is 7.878 × 1010 atoms/s.]

Question 11. Obtain approximately the ratio of the nuclear radii of the gold isotope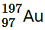and the silver isotope. 

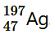Solution : Nuclear radius of the gold isotopeNuclear radius of the silver isotopeMass number of gold, AAu = 197 Mass number of silver, AAg = 107 The ratio of the radii of the two nuclei is related with their mass numbers as:Hence, the ratio of the nuclear radii of the gold and silver isotopes is about 1.23. 

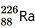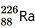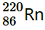Question 12. Find the Q-value and the kinetic energy of the emitted α-particle in the α-decay of (a)and (b). Given m= 226.02540 u,m= 222.01750 u,= 220.01137 u,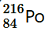= 216.00189 u. 

Solution : (a) Alpha particle decay of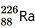emits a helium nucleus. As a result, its mass number reduces to (226 − 4) 222 and its atomic number reduces to (88 − 2) 86. This is shown in the following nuclear reaction.Q-value of emitted α-particle = (Sum of initial mass − Sum of final mass) c2 Where, c = Speed of light It is given that:Q-value = [226.02540 − (222.01750 + 4.002603)] u c2 = 0.005297 u c2 But 1 u = 931.5 MeV/c2 ∴Q = 0.005297 × 931.5 ≈ 4.94 MeV Kinetic energy of the α-particle == (222/226) x 4.94 = 4.85 MeV (b) Alpha particle decay of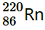is shown by the following nuclear reaction.It is given that: Mass of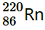= 220.01137 u Mass of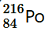= 216.00189 u ∴ Q-value = [220.01137 - (216.00189 +.00260)] × 931.5 ≈ 641 MeV Kinetic energy of the α-particle  = (220-4/220) x 6.41 = 6.29 MeV

Question 13. The radionuclide 11C decays according toThe maximum energy of the emitted positron is 0.960 MeV. Given the mass values:calculate Q and compare it with the maximum energy of the positron emitted Solution : The given nuclear reaction is:Atomic mass of m () = 11.011434 u Atomic mass of= 11.009305 u Maximum energy possessed by the emitted positron = 0.960 MeV The change in the Q-value (ΔQ) of the nuclear masses of thenucleus is given as:....(i) Where, me = Mass of an electron or positron = 0.000548 u c = Speed of light m’ = Respective nuclear masses If atomic masses are used instead of nuclear masses, then we have to add 6 me in the case of ¹¹ Cand 5 me in the case of ¹¹ B. Hence, equation (1) reduces to:∴ΔQ = [11.011434 − 11.009305 − 2 × 0.000548] c2 = (0.001033 c2) u But 1 u = 931.5 Mev/c2 ∴ΔQ = 0.001033 × 931.5 ≈ 0.962 MeV The value of Q is almost comparable to the maximum energy of the emitted positron. 

Question 14. The nucleus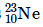decays by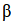emission. Write down the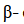decay equation and determine the maximum kinetic energy of the electrons emitted. Given that: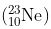= 22.994466 u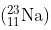= 22.989770 u. 

Solution :

Thedecay equation is(we did not subtract the mass of the electron as it is cancelled because of the presence of one more electron in the sodium atom) Q=0.004696931.5 Q=4.3743 eV The emitted nucleus is way heavier than theparticle and the energy of the antineutrino is also negligible and therefore the maximum energy of the emitted electron is equal to the Q value.

Question 15. The Q value of a nuclear reaction A + b → C + d is defined by Q = [ mA+ mb− mC− md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic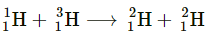. (i)(ii)Atomic masses are given to be

Solution : (i) The given nuclear reaction is:It is given that:According to the question, the Q-value of the reaction can be written as:The negativeQ-value of the reaction shows that the reaction is endothermic. (ii) The given nuclear reaction is:It is given that:The Q-value of this reaction is given asThe positive Q-value of the reaction shows that the reaction is exothermic. Question 16:

Solution : The fission of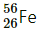can be given as:It is given that:The Q-value of this nuclear reaction is given as:The Q-value of the fission is negative. Therefore, the fission is not possible energetically. For an energetically-possible fission reaction, the Q-value must be positive.

Solution : Average energy released per fission of,Amount of pure, m = 1 kg = 1000 g NA= Avogadro number = 6.023 × 1023 Mass number of= 239 g

Solution :

Question 19. How long can an electric lamp of 100W be kept glowing by fusion of 2.0 kg of deuterium? Take the fusion reaction asSolution : The given fusion reaction is:Amount of deuterium, m = 2 kg 1 mole, i.e., 2 g of deuterium contains 6.023 × 1023 atoms.It can be inferred from the given reaction that when two atoms of deuterium fuse, 3.27 MeV energy is released. ∴Total energy per nucleus released in the fusion reaction:

Question 20. Calculate the height of the potential barrier for a head on collision of two deuterons. (Hint: The height of the potential barrier is given by the Coulomb repulsion between the two deuterons when they just touch each other. Assume that they can be taken as hard spheres of radius 2.0 fm.) Solution : When two deuterons collide head-on, the distance between their centres, d is given as: Radius of 1st deuteron + Radius of 2nd deuteron Radius of a deuteron nucleus = 2 fm = 2 × 10−15 m ∴d = 2 × 10−15 + 2 × 10−15 = 4 × 10−15 m Charge on a deuteron nucleus = Charge on an electron = e = 1.6 × 10−19 C Potential energy of the two-deuteron system:

Question 21. From the relation R = R0A1/3, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e. independent of A). Solution : We have the expression for nuclear radius as: R = R0A1/3 Where, R0 = Constant. A = Mass number of the nucleus

Solution :

Question 23

Solution : Average atomic mass of magnesium, m = 24.312 u

Solution :

Question 25. A source contains two phosphorous radio nuclides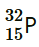(T1/2 = 14.3d) and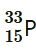(T1/2 = 25.3d). Initially, 10% of the decays come from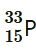. How long one must wait until 90% do so? Solution :

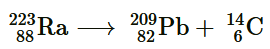
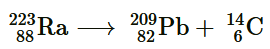Question 26. Under certain circumstances, a nucleus can decay by emitting a particle more massive than an α-particle. Consider the following decay processes:Calculate the Q-values for these decays and determine that both are energetically allowed. Solution : Take aemission nuclear reaction:We know that: Mass ofm1 = 223.01850 u Mass ofm2 = 208.98107 u Mass of, m3 = 14.00324 u Hence, the Q-value of the reaction is given as: Q = (m1 − m2 − m3) c2 = (223.01850 − 208.98107 − 14.00324) c2 = (0.03419 c2) u But 1 u = 931.5 MeV/c2 ∴Q = 0.03419 × 931.5 = 31.848 MeV Hence, the Q-value of the nuclear reaction is 31.848 MeV. Since the value is positive, the reaction is energetically allowed. Now take aemission nuclear reaction:We know that: Mass ofm1 = 223.01850 Mass ofm2 = 219.00948 Mass of, m3 = 4.00260 Q-value of this nuclear reaction is given as: Q = (m1 − m2 − m3) c2 = (223.01850 − 219.00948 − 4.00260) C2 = (0.00642 c2) u = 0.00642 × 931.5 = 5.98 MeV Hence, the Q value of the second nuclear reaction is 5.98 MeV. Since the value is positive, the reaction is energetically allowed. 

Question 27. Consider the fission ofby fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are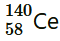and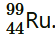. Calculate Q for this fission process. The relevant atomic and particle masses are m=238.05079 u m=139.90543 u m= 98.90594 u Solution : In the fission of, 10 β− particles decay from the parent nucleus. The nuclear reaction can be written as:It is given that: Mass of a nucleusm1 = 238.05079 u Mass of a nucleusm2 = 139.90543 u Mass of a nucleus, m3 = 98.90594 u Mass of a neutronm4 = 1.008665 u Q-value of the above equation,Where, m’ = Represents the corresponding atomic masses of the nuclei= m1 − 92me= m2 − 58me= m3 − 44me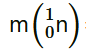= m4Hence, the Q-value of the fission process is 231.007 MeV. 

Question 28. Consider the D−T reaction (deuterium − tritium fusion)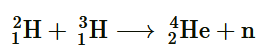(a) Calculate the energy released in MeV in this reaction from the data: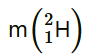= 2.014102 u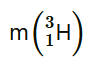= 3.016049 u (b)Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event =average thermal kinetic energy available with the interacting particles = 2(3kT/2); k = Boltzman’s constant, T = absolute temperature.) 

Solution : (a) Take the D-T nuclear reaction:It is given that: Mass of, m1= 2.014102 u Mass of, m2 = 3.016049 u Mass ofm3 = 4.002603 u Mass of, m4 = 1.008665 u Q-value of the given D-T reaction is: Q = [m1 + m2− m3 − m4] c2 = [2.014102 + 3.016049 − 4.002603 − 1.008665] c2 = [0.018883 c2] u But 1 u = 931.5 MeV/c2 ∴Q = 0.018883 × 931.5 = 17.59 MeV (b) Radius of deuterium and tritium, r ≈ 2.0 fm = 2 × 10−15 m Distance between the two nuclei at the moment when they touch each other, d = r + r = 4 × 10−15 m Charge on the deuterium nucleus = e Charge on the tritium nucleus = e Hence, the repulsive potential energy between the two nuclei is given as:Where, ∈0 = Permittivity of free space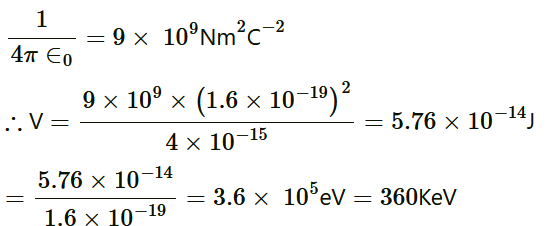Hence, 5.76 × 10−14 J orof kinetic energy (KE) is needed to overcome the Coulomb repulsion between the two nuclei. However, it is given that: KEWhere, k = Boltzmann constant = 1.38 × 10−23 m2 kg s−2 K−1 T = Temperature required for triggering the reactionHence, the gas must be heated to a temperature of 1.39 × 109 K to initiate the reaction. 

Question 29. Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 13.6. You are given that m (198Au) = 197.968233 u m (198Hg) =197.966760 u

Solution : It can be observed from the given γ-decay diagram that γ1 decays from the 1.088 MeV energy level to the 0 MeV energy level. Hence, the energy corresponding to γ1-decay is given as: E1 = 1.088 − 0 = 1.088 MeV hν1= 1.088 × 1.6 × 10−19 × 106 J Where, h = Planck’s constant = 6.6 × 10−34 Js ν1 = Frequency of radiation radiated by γ1-decayIt can be observed from the given γ-decay diagram that γ2 decays from the 0.412 MeV energy level to the 0 MeV energy level. Hence, the energy corresponding to γ2-decay is given as: E2 = 0.412 − 0 = 0.412 MeV hν2= 0.412 × 1.6 × 10−19 × 106 J Where, ν2 = Frequency of radiation radiated by γ2-decay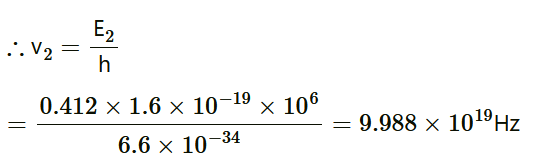It can be observed from the given γ-decay diagram that γ3 decays from the 1.088 MeV energy level to the 0.412 MeV energy level. Hence, the energy corresponding to γ3-decay is given as: E3 = 1.088 − 0.412 = 0.676 MeV hν3= 0.676 × 10−19 × 106 J Where, ν3 = Frequency of radiation radiated by γ3-decayMass of= 197.968233 u Mass of= 197.966760 u 1 u = 931.5 MeV/c2 Energy of the highest level is given as:β1 decays from the 1.3720995 MeV level to the 1.088 MeV level ∴Maximum kinetic energy of the β1 particle = 1.3720995 − 1.088 = 0.2840995 MeV β2 decays from the 1.3720995 MeV level to the 0.412 MeV level ∴Maximum kinetic energy of the β2 particle = 1.3720995 − 0.412 = 0.9600995 MeV 

Question 30. Calculate and compare the energy released by a) fusion of 1.0 kg of hydrogen deep within Sun and b) the fission of 1.0 kg of 235U in a fission reactor. 

Solution : (a) Amount of hydrogen, m = 1 kg = 1000 g 1 mole, i.e., 1 g of hydrogencontains 6.023 × 1023 atoms. ∴1000 g ofcontains 6.023 × 1023 × 1000 atoms. Within the sun, fournuclei combine and form onenucleus. In this process 26 MeV of energy is released. Hence, the energy released from the fusion of 1 kgis:(b) Amount of= 1 kg = 1000 g 1 mole, i.e., 235 g ofcontains 6.023 × 1023 atoms. ∴1000 g ofcontainsIt is known that the amount of energy released in the fission of one atom ofis 200 MeV. Hence, energy released from the fission of 1 kg ofis:Therefore, the energy released in the fusion of 1 kg of hydrogen is nearly 8 times the energy released in the fission of 1 kg of uranium. 

Question 31. Suppose India had a target of producing by 2020 AD, 200,000 MW of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an average, the efficiency of utilization (i.e. conversion to electric energy) of thermal energy produced in a reactor was 25%. How much amount of fissionable uranium would our country need per year by 2020? Take the heat energy per fission of 235U to be about 200MeV. 

Solution : Amount of electric power to be generated, P = 2 × 105 MW 10% of this amount has to be obtained from nuclear power plants. ∴Amount of nuclear power,= 2 × 104 MW = 2 × 104 × 106 J/s = 2 × 1010 × 60 × 60 × 24 × 365 J/y Heat energy released per fission of a 235U nucleus, E = 200 MeV Efficiency of a reactor = 25% Hence, the amount of energy converted into the electrical energy per fission is calculated as:Number of atoms required for fission per year:1 mole, i.e., 235 g of U235 contains 6.023 × 1023 atoms. ∴Mass of 6.023 × 1023 atoms of U235 = 235 g = 235 × 10−3 kg ∴Mass of 78840 × 1024 atoms of U235Hence, the mass of uranium needed per year is 3.076 × 104 kg.

Understand the Core Concepts with Nuclei Class 12 NCERT Solutions 

When you dive into the world of subatomic physics, things get interesting. You aren't just looking at atoms anymore; you're peering into the very heart of matter. The nuclei class 12 ncert solutions 2025 version focuses on giving you a clear path through the revised syllabus. We know that physics can feel like a mountain of math and theory. That's why these solutions break down the heavy lifting into bite-sized pieces.

Physics isn't just about memorizing formulas. It’s about understanding why things happen the way they do at a microscopic level. Whether you’re calculating the radius of a nucleus or figuring out the binding energy per nucleon, you need a reliable guide. The nuclei class 12 ncert solutions new edition ensures that you stay aligned with the latest curriculum changes. We've designed this content to help you build a solid foundation so you don't feel lost during your study sessions.

Understanding Atomic Masses and the Composition of Nucleus

Everything starts with the basics of what makes up a nucleus. You'll find that protons and neutrons, collectively called nucleons, are the stars of the show here. The nuclei class 12 ncert solutions pdf explains how we measure these tiny masses using atomic mass units (u). It’s not practical to use kilograms for something so small. One atomic mass unit is defined as one-twelfth of the mass of a carbon-12 atom.

We use the symbol Z for the atomic number and A for the mass number. You'll often see the notation for a nuclide represented with these variables. It’s a vital part of identifying different isotopes, isobars, and isotones. Isotopes have the same atomic number but different mass numbers. If you're looking at gold or silver, their nuclear properties differ based on this composition. Our solutions provide step-by-step calculations for finding the number of neutrons by simply subtracting Z from A.

Understanding Size of the Nucleus and Nuclear Density

How big is a nucleus? It’s much smaller than the atom itself, yet it contains almost all the mass. Experiments show that the radius of a nucleus is proportional to the cube root of its mass number. You'll use the formula $R = R_0 A^{1/3}$ quite often in your assignments. The constant $R_0$ is approximately $1.2 \times 10^{-15}$ meters.

Interestingly, nuclear density is nearly constant for all nuclei. It doesn't matter if you're looking at a light element or a heavy one; the density remains incredibly high. This suggests that nuclear matter is packed in a very specific way. When you work through the nuclei class 12 ncert solutions, you'll see how to prove this through mathematical derivations. Understanding this concept helps you visualize why the nucleus behaves as a single, tightly bound unit rather than a loose collection of particles.

Mass-Energy Equivalence and Binding Energy Curve

Einstein changed everything with $E=mc^2$. This famous equation tells us that mass can be converted into energy and vice versa. In nuclear physics, we see this when we calculate the mass defect. The mass of a nucleus is always less than the sum of the individual masses of its constituent protons and neutrons. That "missing" mass is what we call the mass defect.

Where does that mass go? It turns into binding energy. This energy keeps the nucleons stuck together against the repulsive forces of the protons. We often look at the binding energy per nucleon to determine how stable an element is. A higher binding energy per nucleon means the nucleus is more tightly bound and stable. The binding energy curve shows that elements like Iron (Fe) are among the most stable in the universe. Our nuclei class 12 ncert solutions 2024 25 guide you through calculating these energy values for various isotopes.

The Strong Nuclear Force and Its Properties

Gravity is weak. Electromagnetism is strong, but it pushes protons apart. So, what holds the nucleus together? The answer is the strong nuclear force. This is the strongest force in nature, yet it has a very short range. It only works over distances of about a few femtometers. If nucleons get too far apart, the force vanishes completely.

The nuclear force is non-central and charge-independent. This means the force between two protons is the same as the force between two neutrons or a proton and a neutron. It’s also an attractive force, but it becomes repulsive if the nucleons get too close to each other. This prevents the nucleus from collapsing in on itself. Understanding these nuances is a vital part of mastering the chapter.

Radioactivity and Decay Laws in Nuclei Class 12 NCERT Solutions

Radioactivity is a spontaneous process. It happens when an unstable nucleus tries to become stable by emitting radiation. You'll study three main types of decay: Alpha, Beta, and Gamma. Alpha decay involves the emission of a helium nucleus. Beta decay involves the emission of electrons or positrons. Gamma decay is the release of high-energy photons.

The law of radioactive decay states that the number of nuclei disintegrating per unit time is proportional to the total number of nuclei present. We use the decay constant and half-life to measure how fast a substance decays. If you want to know how much of a sample remains after a certain period, you'll need these formulas. The nuclei class 12 ncert solutions provide clear examples of how to apply the exponential decay law in practical problems.

Nuclear Fission and Fusion Explained

Energy production relies heavily on nuclear reactions. Nuclear fission is the process where a heavy nucleus splits into two lighter ones, releasing a massive amount of energy. This is the principle behind nuclear reactors. On the other hand, nuclear fusion involves two light nuclei joining to form a heavier one. This happens in the sun and other stars.

Fusion requires extremely high temperatures and pressures. It's often called thermonuclear fusion because of the heat involved. While fission is easier to control on Earth, fusion offers the potential for much cleaner energy in the future. Our solutions compare these two processes, helping you understand the mass-energy transformations that occur in each scenario.

Check out: Class 12th Sample Papers

Benefits of PW CBSE Class 12 Study Material

NCERT & CBSE Syllabus Based
PW CBSE Class 12 study material is designed as per the latest NCERT and CBSE curriculum, ensuring complete exam coverage.

Clear Concept Explanations
Complex topics are explained in simple language with step-by-step solutions for better understanding.

Chapter-wise Notes & Practice Questions
Structured notes, solved examples, and practice questions help in effective revision.

Board Exam Oriented Preparation
Important questions, sample problems, and exam tips support high-scoring preparation.

Ideal for Competitive Exams
The material strengthens concepts needed for entrance exams like JEE and NEET.

Check Out: Class 12 Question Banks

Class 12 Physics Chapter 13 Nuclei FAQs

Q1: What is mass defect in Class 12 Physics?

Mass defect is the difference between the total mass of individual nucleons and the actual mass of the nucleus. This mass difference is converted into binding energy.

Q2: What does the binding energy per nucleon indicate?

It indicates the stability of a nucleus. A higher binding energy per nucleon means the nucleus is more stable and harder to break apart.

Q3: Is the nuclear force dependent on charge?

No, the nuclear force is charge-independent. It acts equally between proton-proton, neutron-neutron, and proton-neutron pairs within its short range.

Q4: What is the significance of the decay constant?

The decay constant represents the probability of decay per unit time for a radioactive nucleus. It determines how quickly a substance will disintegrate.

Q5: Where can I find the nuclei class 12 ncert solutions pdf?

You can access the nuclei class 12 ncert solutions pdf on the PW Store for the latest 2025-26 syllabus.