Area of Square: Definition, Formula, and Examples
The area of a square tells us how much space is enclosed within its four equal sides. It’s a useful measurement in everyday situations such as calculating how much material is needed to cover a floor or how many tiles are required for a wall.
To find the area, you multiply the length of one side by itself. For example, if each side of a square is 6 meters, the area is 6 × 6 = 36 square meters.
Read this blog to understand the steps to calculate the area of a square using its diagonal and perimeter with solved examples.
Check Out: School Books
What is the Area of a Square?
The area of a square is the space covered by a two-dimensional square shape. In other words, it is the region enclosed by the four equal sides of the square. When we represent the area of a square, we always use the square units of measurement, such as square meters, square feet, square inches, etc.
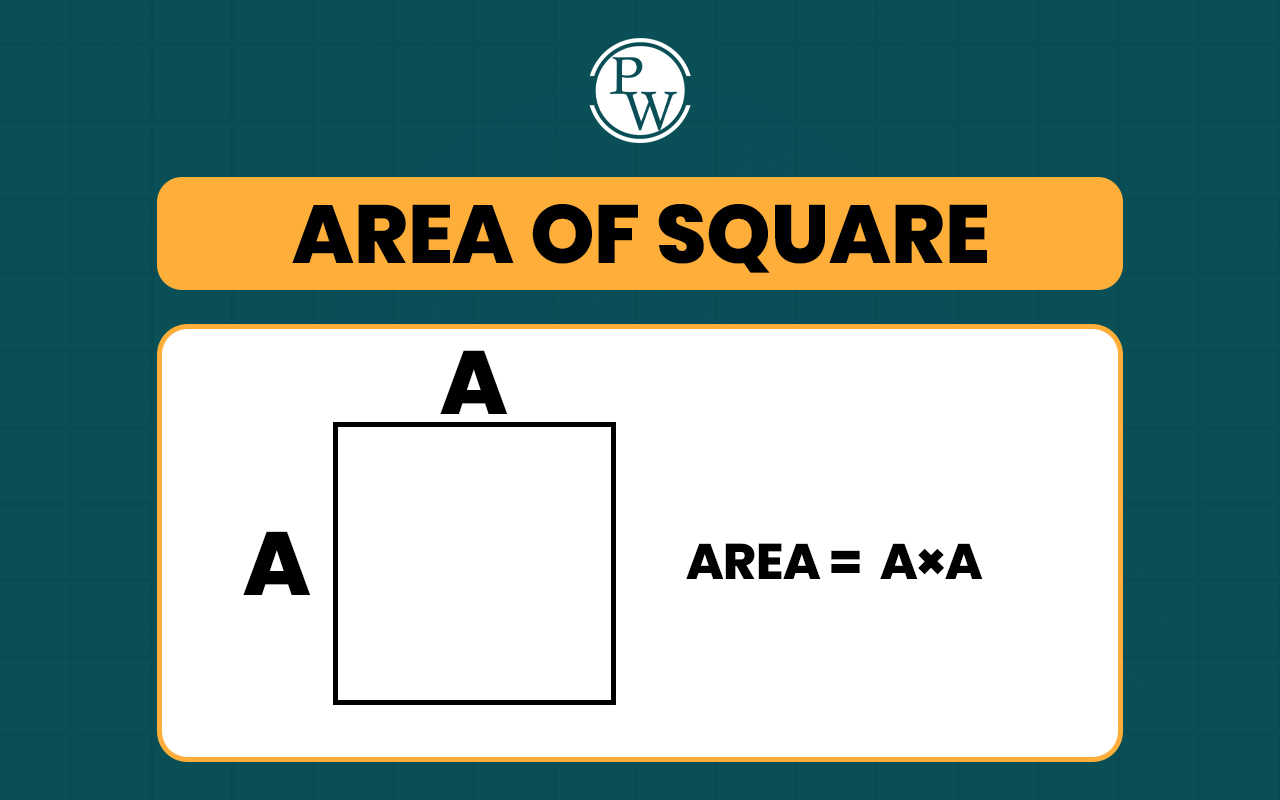
What is the Formula for the Area of a Square?
The formula for the area of a square is very simple, as it is based on only one parameter- the dimension of the side of the square.
A square has four sides, which are all equal, so if we know the dimensions of any one side, we can easily calculate the Area of the square.
The formula for the area of a square is its length multiplied by its width. Now, the length and width of a square are equal dimensions. So, we get the area of the square by multiplying its side by itself or making the square of its side.
Let's consider the dimension of any side of a square is S units. Then the formula for the area of the square is given as:
Area (A) = Side x Side = S x S = S2
For example, if a square shape has each side of 6 cm, then the area of the square is 6 cm x 6 cm = 36 square cm.
Check Out: CBSE Class 10th Books
Formula of the Area of Square Using the Diagonal
The area of a square can be calculated even if we don't know the dimensions of its sides, but the measure of its diagonal is given. Let's understand how to derive the formula for the area of the square when we know the measure of the diagonal.
In the following figure, the measure of each side of the square is S units, and its diagonal is D units.
Now, using the Pythagoras theorem, we can say,
D2 = S2 + S2 = 2S2
Therefore, D = √2S
Or, S = D/√2
Again, we know that the formula for the area of a square is the square of its side.
So, we can write, Area = S2 = (D/√2)2 = D2/2.
Thus, we derive the formula for the area of the square as D2/2, where D is the diagonal.
Let's explain with an example.
We can use the above formula to find the Area of a square with a diagonal measuring 8 cm.
Diagonal of the square (D) = 8 cm
Therefore, the Area of the square is A = D2/2. = (8)2/2 = 64/2 = 32 square cm.
Check Out: Class 9th Books
How to Find the Area of a Square when the Perimeter is Given?
We can find the area of a square even if we don't know the dimensions of its side or the diagonal. But we can calculate the area if the perimeter of the square is given.
Let's understand how to derive the formula for the Area of the square when we know the perimeter of the square.
Suppose 'P' is the Perimeter of a square.
Now, we know that for a quadrilateral, Perimeter = Sum of all sides
If we take the side of the square as ‘a’, we can write P = a + a + a + a = 4a
Therefore, a = P/4
Again, we know that the formula for the area of a square is the square of its side.
Therefore, we can write, Area = a2 = (P/4)2 = P2/16
Let's explain with an example.
The perimeter of the square is 28 cm, and we have to find its Area. Here, we can use the above formula.
The side of the square = 28/4 = 7 cm
Therefore, the area of the square is A = 7 cm x 7 cm = 49 square cm.
Also Check, ICSE Class 10th Books
Area of a Square Solved Examples
1. Find the area of a square whose sides are 12 cm.
Solution: As per the formula for the Area of a square, Area = side x side
Therefore, the Area of this square will be 12 cm x 12cm = 144 square cm.
2. The area of a square plot is 225 square cm. Find the dimensions of the sides of the plot.
Solution: Let's take the sides of the plot = x
Therefore, x2 = 225
Or x = √225 = 15
So, the dimension of the sides of the square plot is 15 cm.
3. Find the area of a square whose diagonal is 6 feet.
Solution: As per the formula of the area of square, if the diagonal is D, then the Area of the square will be D2/2.
Here, the diagonal is 6 feet.
So, the Area of the square is: A = (6)2/2 = 36/2 =18 square feet.
4. Find the area of a square park whose Perimeter is 120 meters.
Solution: The Perimeter of the square park is 120 meters. Therefore, each side of the park has a dimension of 120/4 = 30 meters.
So, the park area is A = (30)2= 900 square meters.
5. A square floor tiling costs Rs. 75/square foot. If the sides of the floor are 10 feet, what will the tiling cost?
Solution: The floor area is A = 10 feet x 10 feet = 100 square feet.
Therefore, the cost of tiling for 100 square feet will be: 100 x 75 =Rs. 7500.
Read More: Basic Math Formulas
Frequently Asked Questions
1. Can we calculate the Perimeter of a square if the area is given?
Ans. Yes, we can calculate the square Perimeter if its Area is given. First, find the side of the square by taking the square root of the Area. Then multiply the side by 4 to get the Perimeter of the square.
2. What happens to the area of a square if the dimensions of its sides are doubled?
Ans. If the sides of a square are doubled, the area will be increased by 4 times.
3. Why is the area of a square expressed in square units?
Ans. The area of a square is calculated by multiplying the two sides. So, the product gives a square value of the sides' units. (cm x cm = square cm)
4. If the perimeters of a square and a rectangle are equal, will their areas be the same?
Ans. No, the areas of a square and a rectangle with equal perimeters will have different areas.











