NCERT Solutions Class 10 Maths Chapter 10 Circles
Circles – Class 10 Maths (Chapter 10) is an important topic for CBSE board exam preparation. Students often look for circles class 10 NCERT solutions to understand the concepts clearly and practise exam-based questions. Class 10 Maths Ch 10 focuses on key ideas related to tangents of a circle and the number of tangents from a point to a circle.
The class 10 circles NCERT solutions explain every question in a step-by-step manner, making it easy for students to follow the logic and apply formulas correctly. These solutions strictly follow the CBSE syllabus and NCERT guidelines, ensuring accurate and exam-oriented preparation. Diagrams and proper explanations help students visualise problems and avoid common mistakes.
Practicing circles class 10 questions answers helps students strengthen their problem-solving skills and improve confidence. The chapter includes both theoretical and numerical questions, which are important from an exam point of view. Regular practice using NCERT-based solutions improves accuracy and time management during exams.
Overall, mastering Circles in Class 10 Maths builds a strong foundation for higher-level geometry and helps students score well in the board examinations.
Check out: CBSE Class 10 Books
NCERT Solutions Class 10 Chapter 10 Circles
Chapter 10 Exercise 10.1
Solve the followings Questions.
1. How many tangents can a circle have?
Answer:
A circle can have infinitely many tangents since there are infinitely many points on the circumference of the circle and at each point of it, it has a unique tangent. 2. Fill in the blanks: (i) A tangent to a circle intersects it in _______________ point(s). (ii) A line intersecting a circle in two points is called a _______________. (iii) A circle can have _______________ parallel tangents at the most. (iv) The common point of a tangent to a circle and the circle is called _______________.
Answer:
(i) one (ii) secant (iii) two (iv) point of contact 3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is: (A) 12 cm (B) 13 cm (C) 8.5 cm (D) √119 cm
Answer:
(D)
We know that the line drawn from the centre of the circle to the tangent is perpendicular to the tangent. ∴OP ⊥ PQ By applying Pythagoras theorem in ΔOPQ,
4. Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Answer:
.png)
AB || CD || EF AB,CD and EF are three parallel lines where EF is the tangent to the circle. Here CD id secant(Intersecting circle at 2 points P and Q)
Read More: NCERT Solutions for Class 10 Maths Chapter 2 Polynomials
Chapter 10 Exercise 10.2
Solve the followings Questions.
In Q 1 to 3, choose the correct option and give justification.
1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is: (A) 7 cm (B) 12 cm (C) 15 cm (D) 24.5 cm
Answer:
(A)
Let O be the centre of the circle. Given that, OQ = 25cm and PQ = 24 cm As the radius is perpendicular to the tangent at the point of contact, Therefore, OP ⊥ PQ Applying Pythagoras theorem in ΔOPQ, we obtain In right triangle OPQ, [By Pythagoras theorem]
OP = 7 cm Therefore, the radius of the circle is 7 cm. Hence, alternative 7 cm is correct. 2. In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to (A) 60° (B) 70° (C) 80° (D) 90°
Answer:
(B) It is given that TP and TQ are tangents. Therefore, radius drawn to these tangents will be perpendicular to the tangents. Thus, OP ⊥ TP and OQ ⊥ TQ ∠OPT = 90º ∠OQT = 90º In quadrilateral POQT, Sum of all interior angles = 360° ∠OPT + ∠POQ +∠OQT + ∠PTQ = 360° ⇒ 90°+ 110º + 90° +∠PTQ = 360° ⇒ ∠PTQ = 70° Hence, alternative 70° is correct. 3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠ POA is equal to (A) 50° (B) 60° (C) 70° (D) 80°
Answer:
(A)It is given that PA and PB are tangents.
Therefore, the radius drawn to these tangents will be perpendicular to the tangents. Thus, OA ⊥ PA and OB ⊥ PB ∠OBP = 90º ∠OAP = 90º In AOBP, Sum of all interior angles = 360° ∠OAP + ∠APB +∠PBO + ∠BOA = 360° 90° + 80° +90º +∠BOA = 360° ∠BOA = 100° In ΔOPB and ΔOPA, AP = BP (Tangents from a point) OA = OB (Radii of the circle) OP = OP (Common side) Therefore, ΔOPB ≅ ΔOPA (SSS congruence criterion) A ↔ B, P ↔ P, O ↔ O And thus, ∠POB = ∠POA
Hence, alternative 50° is correct. 4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer:
Given: CD and EF are the tangents at the end points A and B of the diameter AB of a circle with centre O.
To prove: CD || EF. Proof: CD is the tangent to the circle at the point A. ∴ ∠BAD = 90° EF is the tangent to the circle at the point B. ∴ ∠ABE = 90° Thus, ∠BAD = ∠ABE (each equal to 90°). But these are alternate interior angles. ∴ CD || EF 5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Answer:
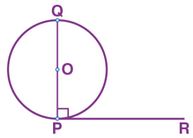Let, O is the centre of the given circle. A tangent PR has been drawn touching the circle at point P. Draw QP ⊥ RP at point P, such that point Q lies on the circle. ∠OPR = 90° (radius ⊥ tangent) Also, ∠QPR = 90° (Given) ∴ ∠OPR = ∠QPR Now, the above case is possible only when centre O lies on the line QP. Hence, perpendicular at the point of contact to the tangent to a circle passes through the centre of the circle. 6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Answer:
Since, the tangent at any point of a circle is perpendicular to radius through the point of contact. Therefore, ∠OPQ = 90° It is given that OQ = 5 cm and PQ = 4 cm
In right ΔOPQ, we have OQ 2 =OP 2 +PQ 2 [Using Pythagoras Theorem] OP 2 = (5) 2 – (4) 2 = 25 – 16 =9 ⇒ OP = 3 cm Hence, the radius of the circle is 3 cm. 7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Answer:
Given Two circles have the same center O and AB is a chord of the larger circle touching the smaller circle at C; also. OA = 5 cm and OC = 3 cm
In Δ OAC,
⇒ AC = 4cm ∴ AB = 2AC (Since perpendicular drawn from the center of the circle bisects the chord) ∴ AB = 2 × 4 = 8cm The length of the chord of the larger circle is 8 cm. 8. A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that: AB + CD = AD + BC
Answer:
We know that the tangents from an external point to a circle are equal. AP = AS ……….(i) BP = BQ ……….(ii) CR = CQ ……….(iii) DR = DS……….(iv) On adding eq. (i), (ii), (iii) and (iv), we get (AP + BP) + (CR + DR) = (AS + BQ) + (CQ + DS) ->AB + CD = (AS + DS) + (BQ + CQ) so,AB + CD = AD + BC 9. In figure, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°.
Answer:
Given: In figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Let us join point O to C. In ΔOPA and ΔOCA, OP = OC (Radii of the same circle) AP = AC (Tangents from point A) AO = AO (Common side) ΔOPA ≅ ΔOCA (SSS congruence criterion) Therefore, P ↔ C, A ↔ A, O ↔ O ∠POA = ∠COA …(i) Similarly, ΔOQB ≅ ΔOCB ∠QOB = ∠COB …(ii) Since POQ is a diameter of the circle, it is a straight line. Therefore, ∠POA + ∠COA + ∠COB + ∠QOB = 180º From equations (i) and (ii),it can be observed that 2∠COA + 2 ∠COB = 180º ∠COA + ∠COB = 90º ∠AOB = 90° 10. Prove that the angel between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Answer:
Let us Consider a circle with centre O. Let P be an external point from which two tangents PA and PB are drawn to the circle which are touching the circle at point A and B respectively and AB is the line segment, joining point of contacts A and B together such that it subtends ∠AOB at center O of the circle. It can be observed that OA ⊥ PA ∴ ∠OAP = 90° Similarly, OB ⊥ PB ∴ ∠OBP = 90° In quadrilateral OAPB, Sum of all interior angles = 360º ∠OAP +∠APB +∠PBO +∠BOA = 360º ⇒ 90º + ∠APB + 90º + ∠BOA = 360º ⇒ ∠APB + ∠BOA = 180º ∴ The angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre. 11. Prove that the parallelogram circumscribing a circle is a rhombus.
Answer:
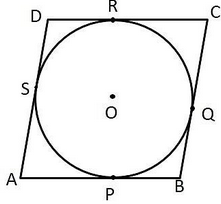Given: ABCD is a parallelogram circumscribing a circle. To Prove: ABCD is a rhombus. Proof: Since, the tangents from an external point to a circle are equal. We know that the tangents drawn to a circle from an exterior point are equal in length. ∴ AP = AS, BP = BQ, CR = CQ and DR = DS. AP + BP + CR + DR = AS + BQ + CQ + DS (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ) ∴ AB + CD = AD + BC or 2AB = 2BC (since AB = DC and AD = BC) ∴ AB = BC = DC = AD. Therefore, ABCD is a rhombus. Hence, proved. 12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.
Answer:
In ΔABC, Length of two tangents drawn from the same point to the circle are equal, ∴ CF = CD = 6cm ∴ BE = BD = 8cm ∴ AE = AF = x We observed that,
13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer:
Let ABCD be a quadrilateral circumscribing a circle with O such that it touches the circle at point P, Q, R, S. Join the vertices of the quadrilateral ABCD to the center of the circle. In ΔOAP and ΔOAS, AP = AS (Tangents from the same point) OP = OS (Radii of the circle) OA = OA (Common side) ΔOAP ≅ ΔOAS (SSS congruence condition) ∴ ∠POA = ∠AOS ⇒∠1 = ∠8 Similarly we get, ∠2 = ∠3 ∠4 = ∠5 ∠6 = ∠7 Adding all these angles, ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 +∠8 = 360º ⇒ (∠1 + ∠8) + (∠2 + ∠3) + (∠4 + ∠5) + (∠6 + ∠7) = 360º ⇒ 2 ∠1 + 2 ∠2 + 2 ∠5 + 2 ∠6 = 360º ⇒ 2(∠1 + ∠2) + 2(∠5 + ∠6) = 360º ⇒ (∠1 + ∠2) + (∠5 + ∠6) = 180º ⇒ ∠AOB + ∠COD = 180º Similarly, we can prove that ∠ BOC + ∠ DOA = 180º Hence, opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Read More: NCERT Solutions for Class 10 Maths Chapter 3
Tangents to a Circle: Fundamental Concepts
A circle and a line in a plane can interact in three ways: they may not intersect at all, the line may cut the circle at two points (a secant), or the line may touch the circle at exactly one point. This third case is known as a Tangent.
According to the chapter 10 maths class 10 ncert solutions, a tangent to a circle is a line that intersects the circle at only one point. This point is referred to as the point of contact.
The source material also mentions that there is only one tangent at a given point on the circle. Additionally, the tangent is a limiting case of a secant when the 2 endpoints of the corresponding chord coincide.
Read More: NCERT Solutions for Class 10 Maths Chapter 4
Key Theorems: Properties of Tangents
The circle ncert solutions class 10 are built upon two primary theorems that students must memorize and learn to prove. These theorems form the basis for solving almost every problem in the exercises.
Theorem 10.1: Perpendicularity of the Tangent
The tangent at any point of a circle is perpendicular to the radius through the point of contact. This means that if OP is the radius and XY is the tangent at point P, then OP \perp XY. This property is frequently used in class 10 maths chapter 10 solutions to apply the Pythagoras Theorem in right-angled triangles formed by the center, the point of contact, and an external point.
Theorem 10.2: Lengths of Tangents
The lengths of tangents drawn from an external point to a circle are equal. If point T is outside the circle, and TP and TQ are tangents touching the circle at P and Q respectively, then TP = TQ. The source material explains this through the congruency of triangles \triangle OPT and \triangle OQT.
Check Out: CBSE Class 10 Sample Papers
Tangents from a Point on and Outside the Circle
Understanding the number of tangents possible from different locations is a common topic in chapter 10 maths class 10 assessments. The source material outlines three specific cases:
-
Inside the Circle: No tangent can be drawn to a circle from a point lying inside it. Any line passing through such a point will be a secant.
-
On the Circle: There is one and only one tangent to a circle passing through a point lying on the circle.
-
Outside the Circle: There are exactly two tangents to a circle from a point lying outside it.
The "Geometric Balance" Perspective
A unique way to view the concepts in Chapter 10 is through the lens of Geometric Balance. While a circle is a symbol of infinite symmetry, a tangent represents a moment of perfect equilibrium where a straight path and a curved path meet at a single, infinitesimal point. Theorem 10.2 (equal tangents) demonstrates a "balance of distance." This framing helps pupils understand that tangents aren't just lines; they are a way to show symmetry in geometry. Drawing two tangents from an outside point creates a perfectly balanced "kite" form (OPTQ). If you think of the chapter as a study of symmetry, the formulae and theorems don't seem like hard and fast rules; instead, they seem like the inherent qualities of a balanced system.
Check Out, CBSE Class 10 Previous Year Papers
Benefits of PW CBSE Class 10 Maths Study Material
Simple and Clear Concepts
PW CBSE Class 10 Maths Study Material explains each topic in easy language with step-by-step solutions. This helps students understand concepts clearly and reduces fear of Maths.
Based on Latest CBSE Syllabus
The content is fully aligned with the latest CBSE and NCERT syllabus, ensuring students focus only on exam-important topics.
Strong Practice Support
The study material includes solved examples, practice questions, and previous years’ questions to improve accuracy and speed.
Easy Revision
Chapter-wise summaries, important formulas, and quick notes make revision simple and effective before exams.
Boosts Exam Confidence
Regular practice and clear understanding help students feel confident and perform better in Class 10 board exams.
Check Out: CBSE Class 10 Question Banks
Class 10 Maths Chapter 10 Circles FAQs
-
How many lines can touch a circle?
A circle can have an unlimited number of tangents because there are an endless number of points on its edge, and you can draw a tangent line at any of those points. -
What is the place where two circles touch?
The point of contact is the one location where a tangent line reaches the edge of the circle. At this point, the radius is always at a right angle to the tangent. -
Are two tangents able to be parallel to each other?
Yes, a circle can only contain two parallel tangents at a time, and these must be drawn at the ends of a diameter. -
How can we figure out how long a tangent is from a point outside?
Theorem 10.1 tells us that the radius is at a right angle to the tangent. We make a right-angled triangle by connecting the center of the circle to the outside point. Then we can utilize the Pythagorean Theorem: (Radius)^2 + (Tangent Length)^2 = (Distance from Center to External Point)^2. -
What is the difference between a tangent and a secant?
A secant is a line that crosses a circle at two different locations, which means it goes through the circle. A tangent is a line that touches the circle at only one point.
