NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

NCERT Solutions for Class 10 Maths Chapter 8

Class 10 Maths Chapter 8, Introduction to Trigonometry, is one of the most interesting and useful chapters in the syllabus. It introduces students to trigonometric ratios like sine, cosine, and tangent, and shows how these can be used to find unknown sides and angles in a right-angled triangle. The concepts in Class 10th Chapter 8 Trigonometry are easy to connect with real life too, such as measuring heights, distances, or angles in everyday situations. Learning this chapter helps students develop logical thinking and accuracy in solving mathematical problems.

The CBSE Class 10 board exams for 2026 are expected to be held in February–March, so this is a good time to start practising regularly. The NCERT Solutions for Class 10 Maths Chapter 8 are a great support for revision, as they provide clear, step-by-step answers to every question from the textbook. These solutions make the concepts simpler to understand and help students prepare with confidence for their Class 10 Maths Chapter 8 Introduction to Trigonometry exam.

Check Out: CBSE Class 10 Books

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.1

Below is the NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.1 Solve the followings

Questions. 1. In Δ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine : (i) sin A, cos A (ii) sin C, cos C

Answer:

Let us draw a right angled triangle ABC, right angled at B. Using Pythagoras theorem,(i)(ii), 

2. In adjoining figure, find tan P – cot R.

Answer:

3. If sin A =3/4, calculate cos A and tan A.

Answer:

Given: A triangle ABC in whichB =90 We know that sin A = BC/AC = 3/4 Let BC be 3k and AC will be 4k where k is a positive real number. By Pythagoras theorem we get, AC ² = AB ² + BC ² (4k) ² = AB ² + (3k) ² 16k ² - 9k ² = AB ² AB ² = 7k ² AB = √7 k cos A = AB/AC = √7 k/4k = √7/4 tan A = BC/AB = 3k/√7 k = 3/√7 

4. Given 15 cot A = 8, find sin A and sec A.

Answer:

Let ΔABC be a right-angled triangle, right-angled at B. We know that cot A = AB/BC = 8/15   (Given) Let AB be 8k and BC will be 15k where k is a positive real number. By Pythagoras theorem we get, AC ² = AB ² + BC ² AC ² = (8k) ² + (15k) ² AC ² = 64k ² + 225k ² AC ² = 289k ² AC = 17 k sin A = BC/AC = 15k/17k = 15/17 sec A = AC/AB = 17k/8 k = 17/8 

5. If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.

Answer:

cos A = cos But

6. If cot θ =7/8, evaluate : (i)(1+sin θ )(1-sin θ)/(1+cos θ)(1-cos θ) (ii) cot ² θ

Answer:

Consider a triangle ABC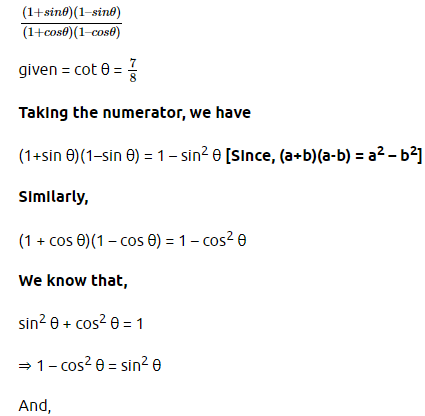(ii)

7. If 3cot A = 4/3 , check whether (1-tan ² A)/(1+tan ² A) = cos ² A – sin ² A or not.

Answer:

Consider a triangle ABC AB=4cm, BC= 3cm.And

8. In triangle ABC, right-angled at B, if tan A =1/√3 find the value of: (i) sin A cos C + cos A sin C (ii) cos A cos C – sin A sin C

Answer:

Consider a triangle ABC in which. (i)(ii)

9. In Δ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.

Answer:

Given that, PR + QR = 25 , PQ = 5 Let PR be x.  ∴ QR = 25 - x By Pythagoras theorem , PR2 = PQ ² + QR ² x ² = (5)2 + (25 - x) ² x ² = 25 + 625 + x ² - 50x 50x = 650 x = 13 ∴ PR = 13 cm QR = (25 - 13) cm = 12 cm sin P = QR/PR = 12/13 cos P = PQ/PR = 5/13 tan P = QR/PQ = 12/5 

10. State whether the following are true or false. Justify your answer. (i) The value of tan A is always less than 1. (ii) sec A = 12/5 for some value of angle A. (iii) cos A is the abbreviation used for the cosecant of angle A. (iv) cot A is the product of cot and A. (v) sin θ = 4/3 for some angle θ.

Answer:

i) False. In ΔABC in which ∠B = 90º, AB = 3, BC = 4 and AC = 5 Value of tan A = 4/3 which is greater than. The triangle can be formed with sides equal to 3, 4 and hypotenuse = 5 as it will follow the Pythagoras theorem. AC ² = AB ² + BC ² 5 ² = 3 ² + 4 ² 25 = 9 + 16 25 = 25 (ii) True. Let a ΔABC in which ∠B = 90º,AC be 12k and AB be 5k, where k is a positive real number. By Pythagoras theorem we get, AC ² = AB ² + BC ² (12k) ² = (5k) ² + BC ² BC ² + 25k ² = 144k ² BC ² = 119k ² Such a triangle is possible as it will follow the Pythagoras theorem. (iii) False. Abbreviation used for cosecant of angle A is cosec A.cos A is the abbreviation used for cosine of angle A. (iv) False. cot A is not the product of cot and A. It is the cotangent of ∠A. (v) False. sin θ = Height/Hypotenuse We know that in a right angled triangle, Hypotenuse is the longest side. ∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.

Check Out: CBSE Class 10 Sample Papers

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.2

Below is the NCERT Solutions for Class 10 Maths Chapter 8 - Introduction to Trigonometry Exercise 8.2

Solve the followings Questions.

1. Evaluate the following : (i) sin 60° cos 30° + sin 30° cos 60° (ii) 2 tan ² 45° + cos ² 30° – sin ² 60° (iii) cos 45°/(sec 30° + cosec 30°) (iv) (sin 30° + tan 45° – cosec 60°)/(sec 30° + cos 60° + cot 45°) (v) (5cos ² 60° + 4sec ² 30° - tan ² 45°)/(sin ² 30° + cos ² 30°)

Answer:

(i) sin 60° cos 30° + sin 30° cos 60°

(ii) 2 tan ² 45° + cos ² 30° – sin ² 60°

(iii) cos 45°/(sec 30° + cosec 30°)

(iv) (sin 30° + tan 45° – cosec 60°)/(sec 30° + cos 60° + cot 45°)

(v) (5cos ² 60° + 4sec ² 30° - tan ² 45°)/(sin ² 30° + cos ² 30°)

2. Choose the correct option and justify your choice : (i) 2tan 30°/1+tan ² 30° = (A) sin 60°   (B) cos 60°  (C) tan 60°  (D) sin 30° (ii) 1-tan ² 45°/1+tan ² 45° = (A) tan 90°   (B) 1        (C) sin 45°      (D) 0 (iii)  sin ² A = 2 sin A is true when A = (A) 0°        (B) 30°      (C) 45°              (D) 60° (iv) 2tan30°/1-tan ² 30° = (A) cos 60°   (B) sin 60°  (C) tan 60°  (D) sin 30°

Answer:

(i) 2tan 30°/1+tan ² 30° = (A) sin 60°   (B) cos 60°  (C) tan 60°  (D) sin 30° =

(ii) 1-tan ² 45°/1+tan ² 45° = (A) tan 90°   (B) 1        (C) sin 45°      (D) 0

(iii) sin ² A = 2 sin A is true when A = (A) 0°        (B) 30°      (C) 45°              (D) 60°

(iv) 2tan30°/1-tan ² 30° = (A) cos 60°   (B) sin 60°  (C) tan 60°  (D) sin 30°

3. If tan (A + B) = √3 and tan (A – B) = 1/√3; 0° < A + B ≤ 90°; A > B, find A and B.

Answer:

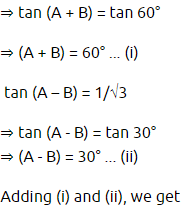
……….(i) 

4. State whether the following are true or false. Justify your answer. (i) sin (A + B) = sin A + sin B. (ii) The value of sin θ increases as θ increases. (iii) The value of cos θ increases as θ increases. (iv) sin θ = cos θ for all values of θ. (v) cot A is not defined for A = 0°.

Answer:

(i) False. Let A = 30° and B = 60°, then sin (A + B) = sin (30° + 60°) = sin 90° = 1 and, sin A + sin B = sin 30° + sin 60° = 1/2 + √3/2 = 1+√3/2 (ii) True. sin 0° = 0 sin 30° = 1/2 sin 45° = 1/√2 sin 60° = √3/2 sin  90° = 1 Thus the value of sin θ increases as θ increases. (iii) False. cos 0° = 1 cos 30° = √3/2 cos 45° = 1/√2 cos 60° = 1/2 cos 90° = 0 Thus the value of cos θ decreases as θ increases. (iv) True. cot A = cos A/sin A cot 0° = cos 0°/sin 0° = 1/0 = undefined.

Check Out: CBSE Class 10 Question Banks

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.3

Below is the NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.3

Solve the followings Questions.

1. Evaluate : (i) sin 18°/cos 72°        (ii) tan 26°/cot 64°        (iii)  cos 48° – sin 42°       (iv)  cosec 31° – sec 59°

Answer:

(i) sin 18°/cos 72° = sin (90° - 18°) /cos 72° = cos 72° /cos 72° = 1 (ii) tan 26°/cot 64° = tan (90° - 36°)/cot 64° = cot 64°/cot 64° = 1 (iii) cos 48° - sin 42° = cos (90° - 42°) - sin 42° = sin 42° - sin 42° = 0 (iv) cosec 31° - sec 59° = cosec (90° - 59°) - sec 59° = sec 59° - sec 59° = 0 

2.  Show that : (i) tan 48° tan 23° tan 42° tan 67° = 1 (ii) cos 38° cos 52° – sin 38° sin 52° = 0

Answer:

(i) tan 48° tan 23° tan 42° tan 67° = tan (90° - 42°) tan (90° - 67°) tan 42° tan 67° = cot 42° cot 67° tan 42° tan 67° = (cot 42° tan 42°) (cot 67° tan 67°) = 1×1 = 1 (ii) cos 38° cos 52° - sin 38° sin 52° = cos (90° - 52°) cos (90°-38°) - sin 38° sin 52° = sin 52° sin 38° - sin 38° sin 52° = 0 

3. If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.

Answer:

tan 2A = cot (A- 18°) ⇒ cot (90° - 2A) = cot (A -18°) Equating angles, ⇒ 90° - 2A = A- 18° ⇒ 108° = 3A ⇒ A = 36° 

4.  If tan A = cot B, prove that A + B = 90°.

Answer:

tan A = cot B ⇒ tan A = tan (90° - B) ⇒ A = 90° - B ⇒ A + B = 90° 

5. If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.

Answer:

sec 4A = cosec (A - 20°) ⇒ cosec (90° - 4A) = cosec (A - 20°) Equating angles, 90° - 4A= A- 20° ⇒ 110° = 5A ⇒ A = 22° 

6. If A, B and C are interior angles of a triangle ABC, then show that sin (B+C/2) = cos A/2

Answer:

7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.

Answer: sin 67° + cos 75° = sin (90° - 23°) + cos (90° - 15°) = cos 23° + sin 15°

Check Out: CBSE Class 10 Previous Year Papers

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.4

Below is the NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.4

Solve the followings Questions.

1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.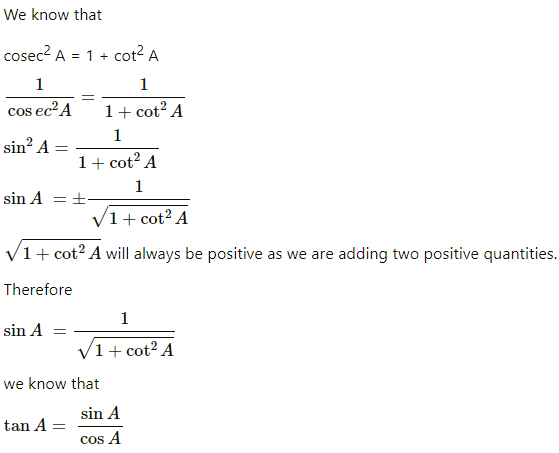

2. Write all the other trigonometric ratios of ∠A in terms of sec A.

Answer:

3. Evaluate : (i) (sin ² 63° + sin ² 27°)/(cos ² 17° + cos ² 73°) (ii)  sin 25° cos 65° + cos 25° sin 65°

Answer:

(i) (sin ² 63° + sin ² 27°)/(cos ² 17° + cos ² 73°)

(ii)  sin 25° cos 65° + cos 25° sin 65°

Choose the correct option. Justify your choice.

4. (i) 9 sec ² A - 9 tan ² A = (A) 1                 (B) 9        (C) 8                (D) 0 (ii) (1 + tan θ + sec θ) (1 + cot θ - cosec θ) (A) 0                 (B) 1        (C) 2                (D) - 1 (iii) (secA + tanA) (1 - sinA) = (A) secA           (B) sinA   (C) cosecA      (D) cosA (iv) 1+tan ² A/1+cot ² A = (A) sec ² A          (B) -1      (C) cot ² A                (D) tan ² A

Answer:

(i) (i) 9 sec ² A - 9 tan ² A = (A) 1                 (B) 9        (C) 8                (D) 0

(ii) (1 + tan θ + sec θ) (1 + cot θ - cosec θ) (A) 0                 (B) 1        (C) 2                (D) - 1

(iii) (secA + tanA) (1 - sinA) = (A) secA           (B) sinA   (C) cosecA      (D) cosA

(iv) 1+tan ² A/1+cot ² A = (A) sec ² A          (B) -1      (C) cot ² A                (D) tan ² A

5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined. (i) (cosec θ - cot θ) ² = (1-cos θ)/(1+cos θ) (ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A (iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ [Hint : Write the expression in terms of sin θ and cos θ] (iv) (1 + sec A)/sec A = sin ² A/(1-cos A) [Hint : Simplify LHS and RHS separately] (v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A,using the identity cosec ² A = 1+cot ² A. (vi) √1 + sin A/1 - sin A = sec A+ tan A (vii) (sin θ - 2sin ³ θ)/(2cos ³ θ-cos θ) = tan θ (viii) (sin A + cosec A) ² + (cos A + sec A) ² = 7+tan ² A+cot ² A (ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA) [Hint : Simplify LHS and RHS separately] (x) (1+tan ² A/1+cot ² A) = (1-tan A/1-cot A) ² = tan ² A

Answer:

(i) (cosec θ - cot θ) ² = (1-cos θ)/(1+cos θ)

(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A

(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ [Hint : Write the expression in terms of sin θ and cos θ]

(iv) (1 + sec A)/sec A = sin ² A/(1-cos A) [Hint : Simplify LHS and RHS separately]

(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A,using the identity cosec ² A = 1+cot ² A

(vi) √1 + sin A/1 - sin A = sec A+ tan A

LHS = 1 + sin A/(1 - sin A) .....(1) Multiplying and dividing by (1 + sin A) ⇒ (1 + sin A)(1 + sin A/1 - sin A)(1 + sin A) = (1 + sin A)²/(1 - sin² A) [a² - b² = (a - b)(a + b)] = (1 + sinA)/1 - sin² A = 1 + sin A/cos² A = 1 + sin A/cos A = 1/cos A + sin A/cos A = sec A + tan A = R.H.S (vii) (sin θ - 2sin ³ θ)/(2cos ³ θ-cos θ) = tan θ

(viii) (sin A + cosec A) ² + (cos A + sec A) ² = 7+tan ² A+cot ² A

(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA) [Hint : Simplify LHS and RHS separately]

(x) (1+tan ² A/1+cot ² A) = (1-tan A/1-cot A) ² = tan ² A

Also Check, CBSE Class 10 Mathematics Handwritten Notes

Summary of Class 10 Maths Chapter 8

• Trigonometry deals with the relationship between the sides and angles of a right-angled triangle.

• Trigonometric ratios introduced: sin θ = opposite/hypotenuse, cos θ = adjacent/hypotenuse, tan θ = opposite/adjacent.

• Reciprocal ratios: cosec θ = 1/sin θ, sec θ = 1/cos θ, cot θ = 1/tan θ.

• Trigonometric ratios can be used to find unknown sides or angles in right-angled triangles.

• Special angles: 0°, 30°, 45°, 60°, 90°, and their trigonometric values.

• Problems involve height and distance applications, such as calculating heights of poles or trees.

• Trigonometric identities like sin²θ + cos²θ = 1 are introduced.

Read More: Tips on How to Score 95 in Class 10 CBSE Maths Exam

Introduction to Trigonometry FAQs

1. What is Chapter 8 of Class 10 Maths?

It introduces trigonometric ratios and how to use them to solve problems in right-angled triangles.

2. Which trigonometric ratios are taught in this chapter?

Sine, Cosine, Tangent, and their reciprocals: Cosecant, Secant, and Cotangent.

3. Are there special angle values in this chapter?

Yes, trigonometric values for 0°, 30°, 45°, 60°, and 90° are discussed.

4. What are the real-life applications of this chapter?

Calculating heights of buildings, poles, trees, or distances using angles.

5. What is the basic formula of sine?

sin θ = opposite/hypotenuse in a right-angled triangle.